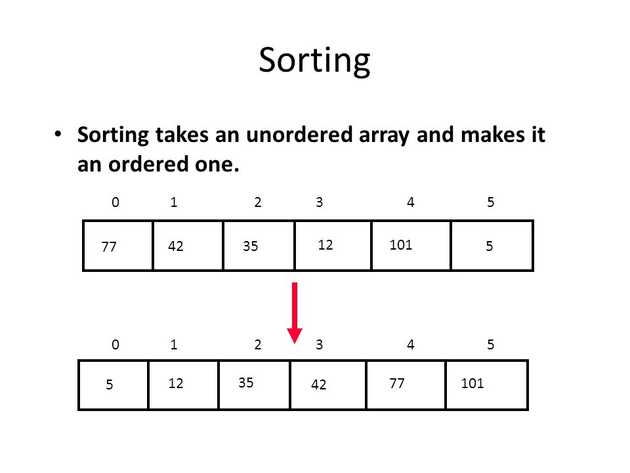
Array sorting is the process of arranging the elements of an array in a specific order, such as ascending or descending order. The order can be based on the value of the elements, or on some other criterion such as the length of the elements in the case of strings.

There are many different algorithms that can be used to sort arrays, and the choice of which one to use can depend on the size of the array, the type of elements it contains, and the desired performance characteristics. Some common array sorting algorithms include quicksort, mergesort, and heapsort.

Common Sorting Algorithms

Selection Sort

Selection sorting works by iterating through the array and selecting the minimum element at each step. The minimum element is then swapped with the current element, and the process is repeated until the array is fully sorted.

//Selection Sort
/**
 * @description This function takes an array as input and sorts it in ascending order using the selection sort algorithm.
 */
const selectionSort = array => {
  for (let i = 0; i < array.length; i++) {
    let minIndex = i
    for (let j = i + 1; j < array.length; j++) {
      if (array[j] < array[minIndex]) {
        minIndex = j
      }
    }
    ;[array[i], array[minIndex]] = [array[minIndex], array[i]]
  }
  return array
}

//Example
let unsortedArray = [5, 2, 7, 1, 3]
let sortedArray = selectionSort(unsortedArray)
console.log(sortedArray) // Output: [1, 2, 3, 5, 7]

Selection sort has a time complexity of O(n^2), which means that the time taken by the algorithm increases quadratically with the size of the array. This makes it less efficient than some other sorting algorithms.

Bubble Sort

Bubble Sorting works by iterating through the array and comparing adjacent elements. If an element is greater than the element after it, the two elements are swapped. This process is repeated until the array is fully sorted.

//Bubble Sort
/**
 * @description This function takes an array as input and sorts it in ascending order using the bubble sort algorithm.
 */
const bubbleSort = array => {
  let swapped = true
  while (swapped) {
    swapped = false
    for (let i = 0; i < array.length; i++) {
      if (array[i] > array[i + 1]) {
        ;[array[i], array[i + 1]] = [array[i + 1], array[i]]
        swapped = true
      }
    }
  }
  return array
}

//Example
let unsortedArray = [5, 2, 7, 1, 3]
let sortedArray = bubbleSort(unsortedArray)
console.log(sortedArray) // Output: [1, 2, 3, 5, 7]

Bubble sort also has a time complexity of O(n^2), which means that the time taken by the algorithm increases quadratically with the size of the array. This makes it less efficient than some other sorting algorithms, such as quicksort and mergesort, which have a time complexity of O(n log n). However, bubble sort is simple to implement and can be a good choice for small arrays or when memory is limited.

Insertion Sort

Insertion sort is a simple sorting algorithm that works by building up a sorted list one element at a time. It iterates through the input array and inserts each element in its correct position in the sorted list.

The algorithm works by iterating over the input array and comparing each element with the elements that come before it. If an element is smaller than the one that comes before it, it is inserted in its correct position. This process continues until the entire array is sorted.

//Insertion sort
/**
 * @description This function takes an array as input and sorts it in ascending order using the insertion sort algorithm.
 */
function insertionSort(array) {
  for (let i = 1; i < array.length; i++) {
    let currentValue = array[i]
    let j
    for (j = i - 1; j >= 0 && array[j] > currentValue; j--) {
      array[j + 1] = array[j]
    }
    array[j + 1] = currentValue
  }
  return array
}

let arr = [5, 2, 4, 6, 1, 3]
console.log(insertionSort(arr)) // Output: [1, 2, 3, 4, 5, 6]

Insertion sort also has a time complexity of O(n^2) in the worst case, which makes it less efficient than other sorting algorithms for large inputs. However, it has a relatively low overhead and can be useful for sorting small arrays or partially sorted arrays.

Merge Sort

Merge sort is a divide and conquer sorting algorithm that works by dividing the input array in half, sorting the two halves, and then merging them back together in a sorted manner.

The merge function takes in two sorted arrays and merges them into a single sorted array. It does this by comparing the first element of each array and adding the smaller of the two to the result array. This process continues until one of the arrays is fully merged into the result array, at which point the remaining elements of the other array are simply appended to the result.

//Merge sort
/**
 * @description This function takes an array as input and sorts it in ascending order using the merge sort algorithm.
 */
function mergeSort(array) {
  if (array.length <= 1) {
    return array
  }

  const middle = Math.floor(array.length / 2)
  const left = array.slice(0, middle)
  const right = array.slice(middle)

  return merge(mergeSort(left), mergeSort(right))
}

function merge(left, right) {
  const result = []
  let leftIndex = 0
  let rightIndex = 0

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex])
      leftIndex++
    } else {
      result.push(right[rightIndex])
      rightIndex++
    }
  }

  return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex))
}

let arr = [5, 2, 4, 6, 1, 3]
console.log(mergeSort(arr)) // Output: [1, 2, 3, 4, 5, 6]

Quick Sort

Quick sort is a divide and conquer sorting algorithm that works by selecting a “pivot” element from the input array and partitioning the other elements into two sub-arrays based on whether they are less than or greater than the pivot. The pivot and the sub-arrays are then sorted recursively using the same process.

function quickSort(array, left, right) {
  if (left < right) {
    const pivotIndex = partition(array, left, right)
    quickSort(array, left, pivotIndex - 1)
    quickSort(array, pivotIndex + 1, right)
  }
  return array
}

function partition(array, left, right) {
  const pivot = array[right]
  let i = left
  for (let j = left; j < right; j++) {
    if (array[j] < pivot) {
      ;[array[i], array[j]] = [array[j], array[i]]
      i++
    }
  }
  ;[array[i], array[right]] = [array[right], array[i]]
  return i
}

let arr = [5, 2, 4, 6, 1, 3]
console.log(quickSort(arr, 0, arr.length - 1)) // Output: [1, 2, 3, 4, 5, 6]

The partition function in the example above selects the last element of the input array as the pivot and rearranges the other elements in the array such that all elements less than the pivot are placed before it and all elements greater than the pivot are placed after it. The pivot is then returned to its correct position in the sorted array by swapping it with the element at the partition index.

Quick sort has a time complexity of O(n log(n)) in the average case and O(n^2) in the worst case. It is generally faster than merge sort and can be implemented in-place (i.e., without requiring additional space), which makes it a good choice for sorting large arrays on devices with limited memory. However, it is not a stable sort, meaning that the order of elements that compare as equal may not be preserved in the sorted output.

Conclusion

Ultimately, the best sorting technique to use will depend on the specific requirements of your application, such as the size and type of the input array, the amount of available memory, and the required stability of the sort. It is often a good idea to benchmark different sorting techniques to determine the most efficient solution for your specific use case.